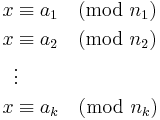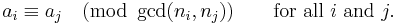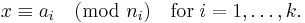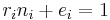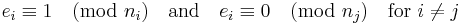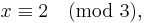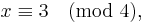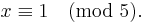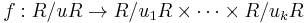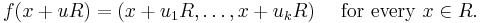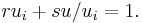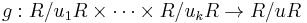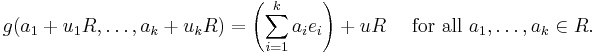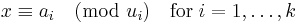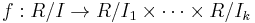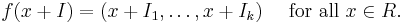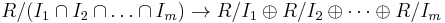Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.
Contents |
Theorem statement
The original form of the theorem, contained in a third-century AD book Sun Zi suanjing (孙子算经 The Mathematical Classic by Sun Zi) by Chinese mathematician Sun Tzu and later republished in a 1247 book by Qin Jiushao, the Shushu Jiuzhang (數書九章 Mathematical Treatise in Nine Sections) is a statement about simultaneous congruences (see modular arithmetic).
Suppose n1, n2, …, nk are positive integers which are pairwise coprime. Then, for any given integers a1,a2, …, ak, there exists an integer x solving the system of simultaneous congruences
Furthermore, all solutions x to this system are congruent modulo the product N = n1n2…nk.
Hence 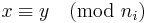 for all
for all 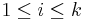 , if and only if
, if and only if 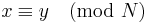 .
.
Sometimes, the simultaneous congruences can be solved even if the ni's are not pairwise coprime. A solution x exists if and only if:
All solutions x are then congruent modulo the least common multiple of the ni.
An alternative method for solving similar systems of equations was described by Aryabhata (6th century; see Kak 1986). Special cases of the Chinese remainder theorem were also known to Brahmagupta (7th century), and appear in Fibonacci's Liber Abaci (1202).
A constructive algorithm to find the solution
The following algorithm only applies if the 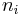 's are pairwise coprime. (For simultaneous congruences when the moduli are not pairwise coprime, the method of successive substitution can often yield solutions.)
's are pairwise coprime. (For simultaneous congruences when the moduli are not pairwise coprime, the method of successive substitution can often yield solutions.)
Suppose, as above, that a solution is required for the system of congruences:
Again, to begin, the product 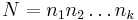 is defined. Then a solution x can be found as follows.
is defined. Then a solution x can be found as follows.
For each i the integers 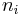 and
and 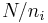 are coprime. Using the extended Euclidean algorithm we can find integers
are coprime. Using the extended Euclidean algorithm we can find integers  and
and 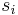 such that
such that 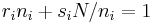 . Then, choosing the label
. Then, choosing the label 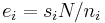 , the above expression becomes:
, the above expression becomes:
Consider 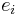 . The above equation guarantees that its remainder, when divided by
. The above equation guarantees that its remainder, when divided by 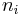 , must be 1. On the other hand, since it is formed as
, must be 1. On the other hand, since it is formed as 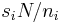 , the presence of
, the presence of  guarantees that it's evenly divisible by any
guarantees that it's evenly divisible by any 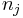 so long as
so long as 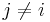 .
.
Because of this, combined with the multiplication rules allowed in congruences, one solution to the system of simultaneous congruences is:
For example, consider the problem of finding an integer x such that
Using the extended Euclidean algorithm for x modulo 3 and 20 [4×5], we find (−13) × 3 + 2 × 20 = 1, i.e. e1 = 40. For x modulo 4 and 15 [3×5], we get (−11) × 4 + 3 × 15 = 1, i.e. e2 = 45. Finally, for x modulo 5 and 12 [3×4], we get 5 × 5 + (−2) × 12 = 1, i.e. e3 = −24. A solution x is therefore 2 × 40 + 3 × 45 + 1 × (−24) = 191. All other solutions are congruent to 191 modulo 60, [3 × 4 × 5 = 60] which means that they are all congruent to 11 modulo 60.
NOTE: There are multiple implementations of the extended Euclidean algorithm which will yield different sets of 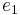 ,
, 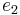 , and
, and 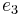 . These sets however will produce the same solution i.e. 11 modulo 60.
. These sets however will produce the same solution i.e. 11 modulo 60.
Statement for principal ideal domains
For a principal ideal domain R the Chinese remainder theorem takes the following form: If u1, ..., uk are elements of R which are pairwise coprime, and u denotes the product u1...uk, then the quotient ring R/uR and the product ring R/u1R× ... × R/ukR are isomorphic via the isomorphism
such that
This isomorphism is unique; the inverse isomorphism can be constructed as follows. For each i, the elements ui and u/ui are coprime, and therefore there exist elements r and s in R with
Set ei = s u/ui. Then the inverse of f is the map
such that
Note that this statement is a straightforward generalization of the above theorem about integer congruences: the ring Z of integers is a principal ideal domain, the surjectivity of the map f shows that every system of congruences of the form
can be solved for x, and the injectivity of the map f shows that all the solutions x are congruent modulo u.
Statement for general rings
The general form of the Chinese remainder theorem, which implies all the statements given above, can be formulated for commutative rings and ideals. If R is a commutative ring and I1, ..., Ik are ideals of R which are pairwise coprime (meaning that Ii + Ij = R whenever i ≠ j), then the product I of these ideals is equal to their intersection, and the quotient ring R/I is isomorphic to the product ring R/I1 x R/I2 x ... x R/Ik via the isomorphism
such that
Applications
- In the RSA algorithm calculations are made modulo
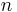 , where
, where 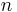 is a product of two large prime numbers
is a product of two large prime numbers  and
and 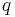 . 1024-, 2048- or 4096-bit integers
. 1024-, 2048- or 4096-bit integers 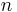 are commonly used, making calculations in
are commonly used, making calculations in 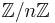 very time-consuming. By the Chinese remainder theorem, however, these calculations can be done in the isomorphic ring
very time-consuming. By the Chinese remainder theorem, however, these calculations can be done in the isomorphic ring  instead. Since
instead. Since  and
and 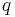 are normally of about the same size, that is about
are normally of about the same size, that is about 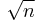 , calculations in the latter representation are much faster. Note that RSA algorithm implementations using this isomorphism are more susceptible to fault injection attacks.
, calculations in the latter representation are much faster. Note that RSA algorithm implementations using this isomorphism are more susceptible to fault injection attacks.
- The Chinese remainder theorem may also be used to construct an elegant Gödel numbering for sequences, which is needed to prove Gödel's incompleteness theorems.
- The following example shows a connection with the classic polynomial interpolation theory. Let r complex points ("interpolation nodes")
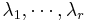 be given, together with the complex data
be given, together with the complex data 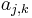 , for all
, for all 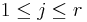 and
and 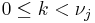 . The general Hermite interpolation problem asks for a polynomial
. The general Hermite interpolation problem asks for a polynomial ![\textstyle P(x)\in \C[x]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/892dd428009cd6c88d21b5684b63e94a.png) taking the prescribed derivatives in each node
taking the prescribed derivatives in each node 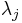 :
:
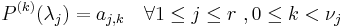 .
.- Introducing the polynomials
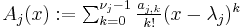 ,
,- the problem may be equivalently reformulated as a system of
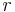 simultaneous congruences:
simultaneous congruences: 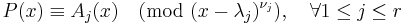 .
.- By the Chinese remainder theorem in the principal ideal domain
![\textstyle\C[x]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/bb457b423b31e79bdfdbde02ca60ed16.png) , there is a unique such polynomial
, there is a unique such polynomial 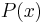 with degree
with degree 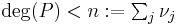 . A direct construction, in analogy with the above proof for the integer number case, can be performed as follows. Define the polynomials
. A direct construction, in analogy with the above proof for the integer number case, can be performed as follows. Define the polynomials 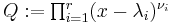 and
and 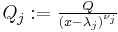 . The partial fraction decomposition of
. The partial fraction decomposition of  gives r polynomials
gives r polynomials 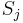 with degrees
with degrees 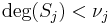 such that
such that 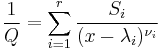 ,
,- so that
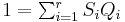 . Then a solution of the simultaneous congruence system is given by the polynomial
. Then a solution of the simultaneous congruence system is given by the polynomial 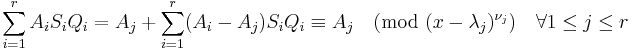 ;
;- and the minimal degree solution is this one reduced modulo
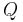 , that is the unique with degree less than n.
, that is the unique with degree less than n.
- The Chinese remainder theorem can also be used in Secret sharing, which consists of distributing a set of shares among a group of people who, all together (but no one alone), can recover a certain secret from the given set of shares. Each of the shares is represented in a congruence, and the solution of the system of congruences using the Chinese remainder theorem is the secret to be recovered. Secret Sharing using the Chinese Remainder Theorem uses, along with the Chinese remainder theorem, special sequences of integers that guarantee the impossibility of recovering the secret from a set of shares with less than a certain cardinality.
- The Good-Thomas fast Fourier transform algorithm exploits a re-indexing of the data based on the Chinese remainder theorem. We refer to the main article Prime-factor FFT algorithm.
- Dedekind's theorem on the linear independence of characters states (in one of its most general forms) that if
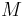 is a monoid and
is a monoid and 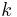 is an integral domain, then any finite family
is an integral domain, then any finite family 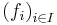 of distinct monoid homomorphisms
of distinct monoid homomorphisms 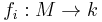 (where the monoid structure on
(where the monoid structure on 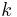 is given by multiplication) is linearly independent, i. e. every family
is given by multiplication) is linearly independent, i. e. every family 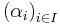 of elements
of elements 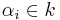 satisfying
satisfying 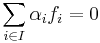 must be equal to the family
must be equal to the family 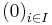 .
.
- Proof using the Chinese Remainder Theorem: First, assume that
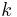 is a field (otherwise, replace the integral domain
is a field (otherwise, replace the integral domain 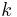 by its quotient field, and nothing will change). We can linearly extend the monoid homomorphisms
by its quotient field, and nothing will change). We can linearly extend the monoid homomorphisms 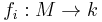 to
to 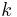 -algebra homomorphisms
-algebra homomorphisms ![F_i:k\left[M\right]\to k](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e324725799553d97ffdfe19dc9db5bcd.png) , where
, where ![k\left[M\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ac33c8178bdb9267d5a398852f22c40e.png) is the monoid ring of
is the monoid ring of 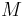 over
over 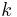 . Then, the condition
. Then, the condition 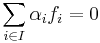 yields
yields 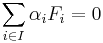 by linearity. Now, we notice that if
by linearity. Now, we notice that if 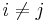 are two elements of the index set
are two elements of the index set 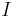 , then the two
, then the two 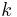 -linear maps
-linear maps ![F_i:k\left[M\right]\to k](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e324725799553d97ffdfe19dc9db5bcd.png) and
and ![F_j:k\left[M\right]\to k](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/62323981f5f90b7c6d15d91ebbdee0f9.png) are not proportional to each other (because if they were, then
are not proportional to each other (because if they were, then  and
and 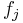 would also be proportional to each other, and thus equal to each other since
would also be proportional to each other, and thus equal to each other since 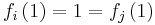 (since
(since  and
and 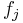 are monoid homomorphisms), contradicting the assumption that they be distinct). Hence, their kernels
are monoid homomorphisms), contradicting the assumption that they be distinct). Hence, their kernels 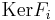 and
and 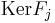 are distinct. Now,
are distinct. Now, 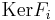 is a maximal ideal of
is a maximal ideal of ![k\left[M\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ac33c8178bdb9267d5a398852f22c40e.png) for every
for every 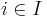 (since
(since ![k\left[M\right] / \mathrm{Ker} F_i\cong F_i\left(k\left[M\right]\right)=k](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/7c8e9c5d43c9d3b6eb46183474a52436.png) is a field), and the ideals
is a field), and the ideals 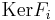 and
and 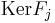 are coprime whenever
are coprime whenever 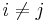 (since they are distinct and maximal). The Chinese Remainder Theorem (for general rings) thus yields that the map
(since they are distinct and maximal). The Chinese Remainder Theorem (for general rings) thus yields that the map ![\phi: k\left[M\right] / K\to \prod_{i\in I}k\left[M\right] / \mathrm{Ker} F_i](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e521b8523019c5136b45d4d436512910.png)
- given by
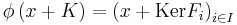 for all
for all ![x\in k\left[M\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c8667492930f1eb307e1f464f6d87677.png)
- is an isomorphism, where
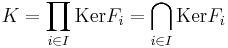 . Consequently, the map
. Consequently, the map ![\Phi: k\left[M\right]\to \prod_{i\in I}k\left[M\right] / \mathrm{Ker} F_i](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/83e72ca25e340e3db003765a3d5b3333.png)
- given by
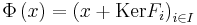 for all
for all ![x\in k\left[M\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c8667492930f1eb307e1f464f6d87677.png)
- is surjective. Under the isomorphisms
![k\left[M\right] / \mathrm{Ker} F_i\to F_i\left(k\left[M\right]\right)=k](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9b6b3eac7720cd6c1d91ee111e319931.png) , this map
, this map  corresponds to the map
corresponds to the map ![\psi: k\left[M\right]\to \prod_{i\in I}k](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9b3f9ea364213f9fdabcff978ec00265.png)
- given by
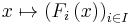 for every
for every ![x\in k\left[M\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c8667492930f1eb307e1f464f6d87677.png) .
.- Now,
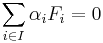 yields
yields 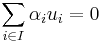 for every vector
for every vector 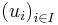 in the image of the map
in the image of the map  . Since
. Since  is surjective, this means that
is surjective, this means that 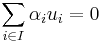 for every vector
for every vector 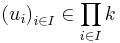 . Consequently,
. Consequently, 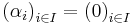 , qed.
, qed.
Non-commutative case: a counter-example
The Chinese remainder theorem does not hold in the non-commutative case. Consider the ring  of non-commutative real polynomials in
of non-commutative real polynomials in 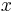 and
and 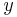 . Let
. Let 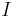 be the principal two-sided ideal generated by
be the principal two-sided ideal generated by 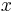 and
and  the principal two-sided ideal generated by
the principal two-sided ideal generated by 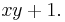 Then
Then 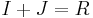 but
but 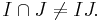
Proof
Observe that 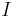 is formed by all polynomials with an
is formed by all polynomials with an 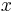 in every term and that every polynomial in
in every term and that every polynomial in  vanishes under the substitution
vanishes under the substitution  . Consider the polynomial
. Consider the polynomial 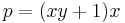 . Clearly
. Clearly 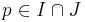 . Define a term in
. Define a term in  as an element of the multiplicative monoid of
as an element of the multiplicative monoid of  generated by
generated by 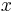 and
and 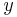 . Define the degree of a term as the usual degree of the term after the substitution
. Define the degree of a term as the usual degree of the term after the substitution  . On the other hand, suppose
. On the other hand, suppose 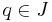 . Observe that a term in
. Observe that a term in 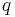 of maximum degree depends on
of maximum degree depends on 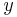 otherwise
otherwise 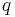 under the substitution
under the substitution  can not vanish. The same happens then for an element
can not vanish. The same happens then for an element 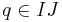 . Observe that the last
. Observe that the last 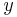 , from left to right, in a term of maximum degree in an element of
, from left to right, in a term of maximum degree in an element of 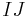 is preceded by more than one
is preceded by more than one 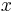 . (We are counting here all the preceding
. (We are counting here all the preceding 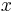 s. e.g. in
s. e.g. in 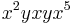 the last
the last 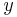 is preceded by
is preceded by 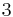
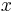 s.) This proves that
s.) This proves that 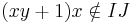 since that last
since that last 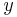 in a term of maximum degree (
in a term of maximum degree (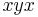 ) is preceded by only one
) is preceded by only one 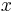 . Hence
. Hence 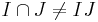 .
.
On the other hand, it is true in general that 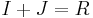 implies
implies 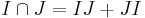 . To see this, note that
. To see this, note that 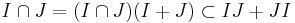 , while the opposite inclusion is obvious. Also, we have in general that, provided
, while the opposite inclusion is obvious. Also, we have in general that, provided  are pairwise coprime two-sided ideals in
are pairwise coprime two-sided ideals in  , the natural map
, the natural map
is an isomorphism. Note that 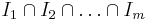 can be replaced by a sum over all orderings of
can be replaced by a sum over all orderings of  of their product (or just a sum over enough orderings, using inductively that
of their product (or just a sum over enough orderings, using inductively that 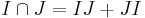 for coprime ideals
for coprime ideals 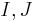 ).
).
See also
- Covering system
- Hasse principle
- Residue number system
- Secret Sharing using the Chinese Remainder Theorem
References
- Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Section 4.3.2 (pp.286–291), exercise 4.6.2–3 (page 456).
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 31.5: The Chinese remainder theorem, pp.873–876.
- Sigler, Laurence E. (trans.) (2002). Fibonacci's Liber Abaci. Springer-Verlag. pp. 402–403. ISBN 0-387-95419-8.
- Kak, Subhash (1986), "Computational aspects of the Aryabhata algorithm", Indian Journal of History of Science 21 (1): 62–71, http://www.ece.lsu.edu/kak/AryabhataAlgorithm.pdf.
External links
- "Chinese Remainder Theorem" by Ed Pegg, Jr., Wolfram Demonstrations Project, 2007.
- Weisstein, Eric W., "Chinese Remainder Theorem" from MathWorld.
- C# program and discussion at codeproject
- University of Hawaii System CRT by Lee Lady